Az egyenes egyenlete átmenő adott pontot

Ha adott konkrét pontokat, például egy (4; 10) és B (1 és 2), akkor az egyenlet megtalálható megoldása az egyenletrendszer.

Ha A és B eltérő első koordináta (abszcissza), az egyenes vonal, amely fekszenek pontok nem párhuzamos az y tengely és az által leírt egyenlettel y = kx + b. Feljebb az egyenletrendszert és oldja meg. Például:

| 10 = 4k + b,
| 2 = k + b.

b = 2 - k
10 = 4k + 2 - k
8 = 3k
k = 8/3

és az egyenes egyenlete adott.

Azonban, mi is meghatározzuk általános forma lineáris egyenlet által kifejezett koordináták A (x1, y1) és B (x2; y2), ha x1 ≠ x2.

b = y2 - kx2
Y1 = kx1 + y2 - kx2
y1 - y2 = kx1 - kx2
y1 - y2 = k (x1 - x2)

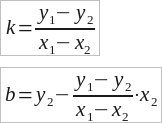
Ismerve b és k. akkor most kap az egyenlet az általános formája:

Az algebrai átalakítás, ez az egyenlet lehet csökkenteni, hogy egy egyszerűbb formában:

.