minta átlaga

Szelektív sredneeznachenie pokazatelpredstavlyaet a statisztikai átlagos értékelés van kísérletileg pszichológiai minőségét.

Ez a becslés jellemzi ennek mértékét a fejlődést általában, a tárgycsoportot alávetett pszicho-diagnosztikai vizsgálat céljából. Összehasonlítva csak az átlagos értékét két vagy több minta, tudjuk ítélni a relatív fejlettségi foka az emberek teszik ki a minta, a becsült minősége.

A minta átlag határozzuk meg a következő képlet segítségével:

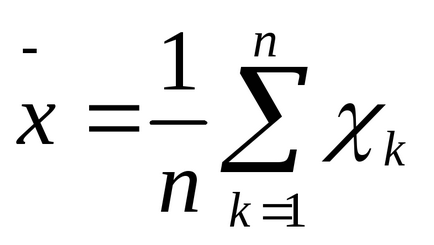
HSR -vyborochnaya átlagos értékét vagy számtani középértéke a minta;

N - alanyok száma a mintában vagy magán psychodiagnostical indexek Itt a számítás alapja az átlagos értéket;

xk- privát érték mutatói egyes tantárgyak. Mindezek a mutatók n, tehát a k index a változó vesz értékek 1-től n-ig;

Σ - elfogadott matematikai jele összegzése a mennyiségek azok a változók, amelyek a jobb ez a jel.

kifejezés

illetőleg azt jelenti, az összeg az összes x k index 1-től n.

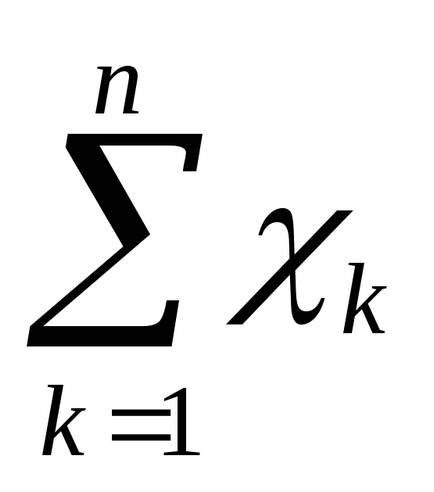
Példa. Tegyük fel, hogy az alkalmazás pszichodiagnosztikai módszer értékelésére bizonyos pszichológiai tulajdonságok közül tíz alany megkaptuk a következő konkrét paraméterek, a fejlettségi foka tulajdonságok az egyes alanyok: x1 = 5 és x2 = 4, x3 = 5, x4 = 6, x5 = 7, x6 = 3, 6 = x7, x8 = 2, X9 = 8 × 10 = 4. Következésképpen, n = 10, és a k index érték módosításához 1-től 10 a fenti képletben. Ezen mintánál a középérték 1 számítva ez a képlet a következő lesz:

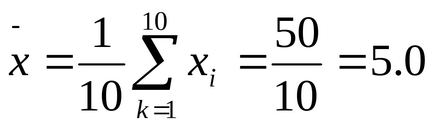
1 Ezt követően, ahogy az szokásos matematikai statisztika, azzal a céllal, hogy csökkentsék a szöveget fogjuk hagyni a „szelektív” és „számtani”, és egyszerűen beszél „átlagos” vagy „átlag”.

A kísérleti psychodiagnosis és pszicho-pedagógiai kutatások átlag általában nem számított pontossággal nagyobb, mint egy vagy két tizedes jegyre, azaz Több mint tized vagy század egy egységet.

A pszichodiagnosztikai felmérés nagy pontosságú számítások nem kötelező, és nincs értelme, ha figyelembe vesszük a közelítő jellegét az értékelések, amelyben keletkeztek, illetve azok megfelelőségét az ilyen becslések a termelés viszonylag pontos számításokat.

Dispersiyakak statisztikai nagyságát jellemzi, hogyan adott értékei eltérnek az átlagos vdannom mintában.

Minél nagyobb a variancia, a nagyobb az eltérés, vagy variációs adatok. Mielőtt bemutatnánk a képlet a variancia kiszámítására, egy példát. Mi használjuk azokat elsődleges adatok, amelyeket korábban adott, és amelyből számítottuk az előző példában, az átlagos érték. Látjuk, hogy ezek mind különbözőek és különböző nemcsak egymással, hanem az átlagtól. Mérjük meg a teljes különbség az átlagos értéket és szórását jellemzi. Ez határozza meg annak érdekében, hogy meg lehessen különböztetni egymástól mennyiségben, azonos átlagos, de eltérő szórás.

Képzeljünk el egy másik, eltér a korábbi mintaértékeket az elsődleges, például 5, 4, 5, 6, 5, 6, 5, 4, 5, 5. Ez könnyen ellenőrizhető, hogy a középérték is egyenlő 5,0. De ebben a mintában, hogy néhány konkrét értékek eltérnek az átlagtól jóval alacsonyabb, mint az első mintában. Mi kifejezetten a diszperziós fok segítségével a különbségeket, amely meghatározza a következő képlet szerint:

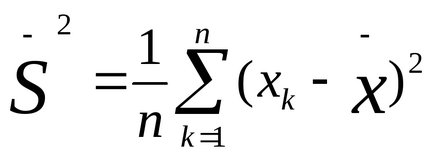
ahol

- minta eltérés, vagy egy diszperzió;

- egy kifejezés, ami azt jelenti, hogy minden xk az elsőtől az utolsóig a mintában kell számítani a különbség a magán- és az átlagos értékeket, építeni ezek a különbségek négyzetének és foglalta;

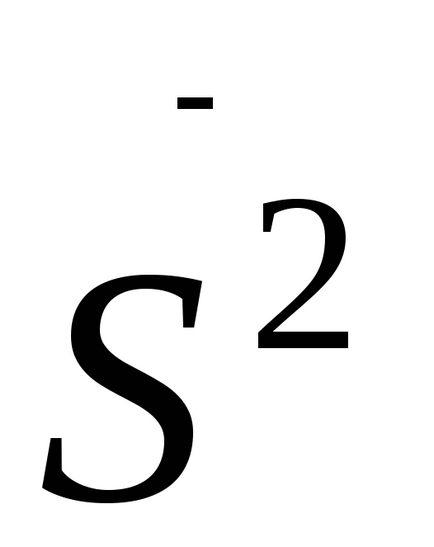
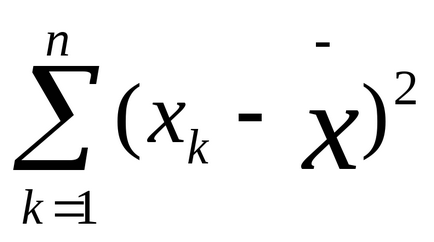
N - alanyok száma a mintában, vagy a kezdeti értékek, amelyekre a variancia kiszámítása.

Megjegyezzük, hogy számos publikáció a diszperzió lehet kijelölni D (x).

Mi határozza meg a variancia két konkrét értékeket a fenti minták, kijelölő rendre a diszperzió indexek 1 és 2:

Látjuk, hogy a szórása a második minta (0,4) lényegesen kisebb szórása az első minta (3.0). Ha nem volt eltérés, nem tudtuk megkülönböztetni a minta adatokat.