A görbületi és a görbületi sugara a pálya - studopediya

A görbület egy görbe, ahol - a forgásszög egy érintőleges a görbe szakasz hossza.

A görbületi sugár - reciprok értékét a görbület:

A görbületi sugár a kör a kör sugara; vonal görbületi sugara végtelen. A görbületi sugara méterben.

Normál pontot, amelynek távolsága egy adott pont a röppálya irányába konkáv görbe a távolból, az úgynevezett görbületi középpontja a görbe megfelel egy adott pont a görbe. A lókusz a görbületi középpontok formák a vonal - eredeti evolután görbe (evolutus (lat) - expandált ;. Voluto - tekercs, tekercs). Kezdeti evolvens görbe képest a evolután (evolventis - unfurling).

♦ Ha a közelítő pályáját a terület (ábra. 2) körív, a közepén fekszik a metszéspontja merőleges kinyert felezőpontja az akkordok és. Korlátozása pont pozíciója nyújtott. mikor. a görbületi középpontja a pálya azon a ponton M.

Ha az R sugár a tekercs, hogy a tekercs a szál visszatartó visszacsévélő egyenes része, a végén a fonalat leírják egy kört evolvensek, nevezetesen megfelelő a pont, amelynél a fonal végét eloldalog kezdődött. Ábra. 3, és megmutatja a evolvens kör sugara. megfelel a jobb szélső kiindulópontja a menet van tekercselve az óramutató járásával ellentétes. Paraméteres egyenletek az evolvens

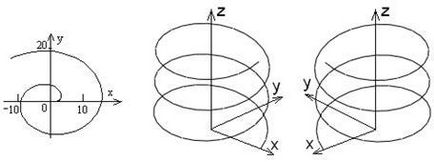
Ábra. 3. evolvens a kör. hélix

Ha ez a görbe közel van a spirál az Arkhimédész, amelynek egyenlete polár-koordinátákkal.

A fogak a kerekek a legtöbb fogaskerekek evolvens profilú, így minimalizálva az elcsúszást, fogat fogért egyszerűsített gyártási fogaskerekek magukat. Az alap profil tartalmazhat evolvens foga ( „scanning”) az alapkör (cm. „Az elmélet a gépek és mechanizmusok”) kapcsolódó kerék.

1.1.15. Természetes triéder (természetes triéder) - triéder épült, a tengelyeket az érintő, normál és binormals. Binormal egység vektort úgy definiáljuk, mint; akkor. Simuló sík átmegy az érintő és normális. A repülőgép, amely a normál és binormal, az úgynevezett merőleges síkban, és a gép tartalmaz binormal és érintőleges - egyengető. Természetes triéder orientált térben alakja szerint a görbe. Az alakjáról információt (geometria a belső ív) lehet használni, hogy vizsgálja meg a anyagi pont mozgását ezen a görbén.

Térbeli görbe, függetlenül annak elhelyezkedését illetően környező tárgyak leírható meghatározásával minden pontján a görbület és csavarodás (görög „kappa”.) A görbe:

Nagysága a torziós ahol - a forgásszög a binormal a terület a görbe hosszát.

A képletek Serret - Frenet:

A görbület - pozitív paraméter. Torziós „helyes” spirál ábrán látható. 3, b pozitív. Torziós a „bal” (. Ábra 3c) - negatív.

1.1.16. Egyenletesen gyorsuló mozgás határozza meg a feltétele a pont

; majd a képletek: