Módszer csomópontok a problémát b5
Van egy csodálatos formula, amely lehetővé teszi számunkra, hogy fontolja meg a terület egy sokszög a rács szinte hiba nélkül. Ez nem is egy képlet, és a jelen tétel. Első pillantásra úgy tűnhet, ijesztő. De ahhoz, hogy megoldja egy pár probléma - és látni fogja, hogy ez a jó funkció. Így megy előre!
Kezdeni, egy olyan új definíció:
Node koordináta halom - a bármely pontján fekvő metszi a függőleges és vízszintes vonalak a rács.
Az első képen a csomópontok általában nincsenek jelölve. 4 vannak kijelölve a második csomópont. Végül, minden 16 egység fel van tüntetve a harmadik kép.
Hogyan kapcsolódik ez a probléma B5? Az a tény, hogy az a sokszög csúcsai az ilyen problémák mindig mesh csomópontok. Ennek következtében a munka a következő tétel:
Tétel. Tekintsük a poligon háló, amelynek csúcsai a csomópontok a rács. Ezután a sokszög területe egyenlő:
ahol n - csomópontok száma egy adott sokszög, k - a csomópontok száma, hogy fekszenek a határ (határ csomópontok).
Példaként vegyünk egy szabályos háromszöget a rács, és próbálja megjegyezni a belső és a határ csomópontokat.
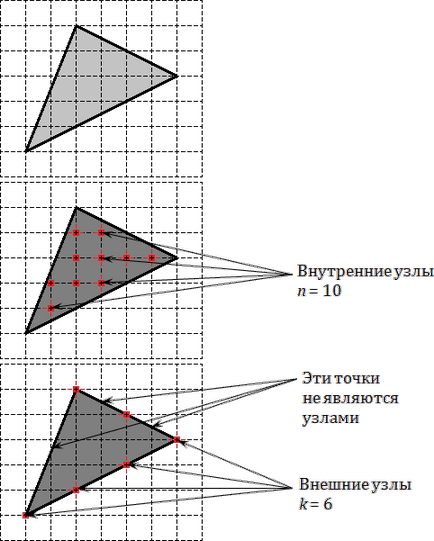
Az első képet adott szabályos háromszöget. A második jelölt a belső alkatrészek, amelyek száma megegyezik a n = 10. A harmadik kép jelölt csomópontok feküdt a határon, már csak k = 6.
Talán sok olvasó nem érti, hogyan kell számolni a n és k. Kezdje belső csomópontokat. Minden tiszta: festeni a háromszög ceruza és látni, hogy hány telek alá került árnyékolás.
Egy kicsit bonyolultabb határ csomópontokat. A határ a sokszög - zárt vonallánc. amely keresztezi a rács sok helyen. A legegyszerűbb módja annak, hogy vegye figyelembe minden „kezdő” pontot, majd megkerülni a többit.
Határ csomópontok csak azokat a pontokat a szaggatott vonal, ahol három vonalak metszik egymást ugyanabban az időben.
- Tény, hogy egy szaggatott vonal;
- A vízszintes vonal a rács;
- A függőleges vonal.
Lássuk, hogyan működik az ilyen feladatokat.
Feladat. Keressen egy háromszög területén, ha a cella mérete 1 x 1 cm-es:
Először is csomópontokat, hogy hazugság a háromszög belsejében, valamint annak határán:
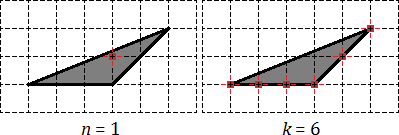
Kiderült, hogy csak egy belső csomópont: n = 1. határoló csomópontok - annyi, mint hat, három egybeesik a csúcsai a háromszög. és három oldalán. Összesen k = 6.
Most tekintsük a területen a következő képlet segítségével:
Ez az! A probléma megoldódott.
Feladat. Find a négyszög területe látható grafikonon papírt a méret a cella 1 cm 1 cm-rel. Response, így négyzetcentiméter.

Ismét megjegyezzük, a belső és a határ csomópontokat. Belső csomópontjai minden n = 2. Határ csomópontok: k = 7, 4 amelyek a csúcsai a négyszög. és még 3 van az oldalán.
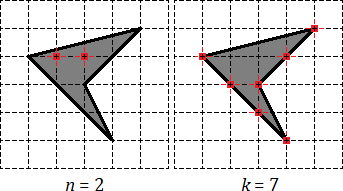
Továbbra is helyettesítheti számokat n és k a képlet nagysága:
Fontos tudnivaló a területeken
De a képlet - ez még nem minden. Nézzük átírni a képlet, így szempontjából a jogot arra, hogy a közös nevező. kapjuk:
A számok n és k - a csomópontok száma, ezek mindig egész szám. Így is, egy egész számlálót. Azt ossza meg a 2, ami azt jelenti, egy fontos tényt:
A terület mindig kifejezett egész szám vagy törtszám. És a végén a frakció mindig „öt tized”: 10,5; 17,5, stb
Így a probléma területen B5 mindig által kifejezett egy egész vagy egy része a forma *** 5. Ha a válasz más, az azt jelenti, hogy valahol a hiba. Tartsa ezt szem előtt, ha megteszi az igazi vizsga a matematika!
- Ingyenes Felkészülés a vizsgára 7 egyszerű, de nagyon hasznos tanulságokat + házi feladat
