Megoldás logaritmikus egyenlőtlenségek

Megoldás logaritmikus egyenlőtlenségek

Megoldás logaritmikus egyenlőtlenségek van sok közös döntés jelzi egyenlőtlenségek:

a) az átállás során logaritmikus hogy expresszió logaritmusának, mi is össze a bázis a alapú logaritmusa az egység;

b) Ha megoldjuk logaritmikus egyenlőtlenség felhasználásával helyettesítő változókat, el kell döntenie, hogy cserére, amíg az elemi egyenlőtlenség.

Van azonban egy lényeges különbség: mivel a logaritmus függvény korlátozott domain, a átmenet logaritmikus expressziós alatt logaritmus, szükséges, hogy figyelembe vegyék a különböző megengedett értékeket.

Ha megoldására logaritmikus egyenletek megtalálja a gyökerei az egyenlet, majd csinál egy átvilágítás, majd megoldásában logaritmikus egyenlőtlenségek száma nem felel meg: ha átmegy a logaritmus expressziós alatt logaritmusát kell rögzíteni DHS egyenlőtlenség.

Szóval A legegyszerűbb logaritmikus egyenlőtlenség formájában:

V, ahol V - egyik jele az egyenlőtlenség: <,>, Vagy ≤ ≥.

Ha a logaritmus bázis egynél nagyobb (), majd megy a logaritmusát a kifejezés alatt logaritmus jele, annak a jele, az egyenlőtlenség fennáll. és az egyenlőtlenség

Ha a logaritmus bázis értéke nullánál nagyobb és kisebb, mint egy (), majd megy a logaritmusát a kifejezés alatt logaritmus jele, annak a jele, az egyenlőtlenség megfordul. és az egyenlőtlenség

Tekintsük a példák oldatok logaritmikus egyenlőtlenségek.

1. Oldja meg az egyenlőtlenséget:

Mint az alap a logaritmus mindkét oldalán az egyenlőtlenség kisebb, mint 1, az átmenet a alatti kifejezés logaritmusa jel, a jele az egyenlőtlenség megfordul. Expression alatt logaritmus kell szigorúan nagyobb, mint nulla. Most viszont, hogy a rendszer:

Figyelem: rámutatni arra, hogy több mint a nulla a kisebb összeg a kifejezések, amelyek alapján a logaritmus jele. Ebben az esetben egy nagyobb kifejezést automatikusan nagyobb, mint nulla.

Mi megoldjuk a rendszer egyenlőtlenségek:

A gyökerek a másodfokú polinom :,

2. Oldja meg az egyenlőtlenséget:

Látjuk, hogy az alapja a logaritmusok 2 hatványai, így tudjuk hozni a logaritmusok azonos bázis. Tesszük ezt a tulajdonságok használatával logaritmus:

Transzfer a logaritmusa negatív együtthatója a bal oldalon a jobb (a többszörösen könnyebb, mint osztás).

Mivel a egyenlőtlenség jelen logaritmusokat ugyanazt a bázist, és az első fokú, tudjuk képviseli mindkét oldalán a egyenlőtlenség mint alapú logaritmusa 2:

Most lépni a logaritmusát a kifejezés alatt logaritmus jele. Az alap nagyobb, mint 1, így a jel az egyenlőtlenség fennáll. Ne feledkezzünk meg a DHS:

3. Oldjuk meg az egyenlőtlenséget:

Ebben az egyenlőtlenség logaritmus ez áll a téren, így ez egy logaritmikus egyenlőtlenségek fogunk dönteni a változás változók.

Először ad logaritmusának az azonos alap:

Bemutatjuk a változás változók:

.

Kapunk egy másodfokú egyenlőtlenség:

Írunk a kettős egyenlőtlenség rendszer:

Csak most, amikor már a rendszer egyszerű egyenlőtlenségek tekintetében, akkor visszatérhet az eredeti változó.

Térjünk át varazheniyam alatt álló logaritmus jele:

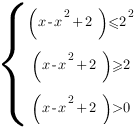
Az utolsó egyenlőtlenség a rendszer - ez DHS egyenlőtlenség. Vegyük észre, hogy ha teljesítik az alábbi második egyenlőtlenség, így nem kell foglalkozni kell.

Az első rendszer az egyenlőtlenség átalakul

Diszkriminánsa ez másodfokú polinom negatív, Senior KOEFFICIENS pozitív, így az egyenlőtlenség igaz minden valós értékeket.

A második egyenlőtlenség alakítjuk formájában innen