logaritmikus egyenlőtlenségek

Mivel a logaritmus alapja nagyobb, mint 1, akkor a jele egyenlőtlenség továbbra is fennáll:

Mivel a logaritmus alapja kevesebb, mint 1, az egyenlőtlenség jele változás:

Átkelés a döntést, és a DHS, van:

Megoldjuk az eljárás időközönként. A gyökér a számláló -. nevező gyökér - ez mindig egy törölt pont, a gyökér a számláló - is törlésre kerül pont, mint egy jel a szigorú. Így.

Mi jár, hogy összehasonlítsuk a logaritmus kifejezések, a jel megmarad: az alap nagyobb, mint 1:

A gyökér a számláló -. nevező gyökér - ezen a ponton kilyukadt mindig a gyökér a számláló - árnyékos helyen, akkor bemegy a döntést jeleként egyenlőtlenség nem szigorú. Így.

Az impozáns megoldásokat DHS kapjuk:

A megoldás a rendszer -

Ennek jeleként egyenlőtlenség laza, akkor a pontokat tartalmazza a megoldás: meg kell képviselni az árnyékos az ábrán. Egyenlőtlenség megoldás :.

Impozáns megoldást a tartományban megengedett értékeket, kapjuk:

A megoldás a rendszer -

Az 1. pont kilyukadt - a gyökere a nevező, 2 pont - a gyökere még sokfélesége, és arra gondolunk, hogy az ilyen pontok az intervallum a jel nem változik! Ezért a megoldás így fog kinézni:

Ez teljes mértékben összhangban van a DHS, így a válasz így lesz:

egyenlőtlenség döntés módszerével racionalizálás:

Bomlanak tényezők:

Megjegyezzük A kapott pontok a koordináta tengely:

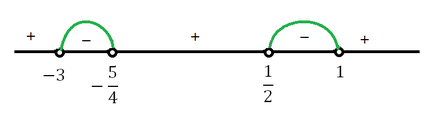
Elhelyezés a döntés DHS, van: