Körülírt egyenlő oldalú háromszög, háromszög

Körülírt egyenlő oldalú háromszög, rendelkezik az összes leírt tulajdonságok tetszőleges háromszög kerülete körül, továbbá, megvannak a saját tulajdonságai.

1) A központ a köré írt kör a háromszög - a metszéspont midperpendiculars az oldalaival.

Mivel a medián, a magasság és a felezővonal egybeesik egy egyenlő oldalú háromszöget. a központja egy egyenlő oldalú háromszög körül a kör metszéspontjában annak mediánértékeknek magasságok és bisectors.

Például az ABC derékszögű háromszög AB = BC = AC = a

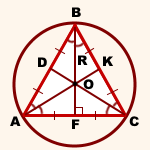
Point O - circumcenter.

AK, BF és CD - medián, a magasság és a felezővonal az ABC háromszög.

2) A távolság a központtól a körülírt kör a csúcsai a háromszög egyenlő a sugár. Amint azt a központjában egy egyenlő oldalú háromszög kör metszéspontjában annak medián és a medián a háromszög a metszéspont vannak osztva arány 2: 1. számítva a felső, a sugara a körülírt kör kétharmada a hossza a medián:

Így, a képlet sugarú köré írt kör az egyenlő oldalú háromszög -

Fordítva, egy egyenlő oldalú háromszöget egymás sugara a körülírt kör -

3) A képlet megtalálásához a terület egy egyenlő oldalú háromszög az oldalára -

Ezért találunk a terület a sugara a körülírt kör:

Így, a képlet négyzet alakú területének a szabályos háromszög sugarának a körülírt kör -

4) Fitneszterem leírt megközelítőleg derékszögű háromszög egybeesik a kör a kör középpontja az ezekben feltüntetett.

5) A sugár a leírt kör körülbelül egy egyenlő oldalú háromszög kétszerese a sugara a beírt kör: