Kényszerített mechanikai rezgések 1

Jelöljük - közötti szög az elmozdulás és a hajtóerő.

Behelyettesítve (3.3.3), (3.3.4) és (3.3.5) a (3.3.1):

Minden kifejezés az utolsó egyenlet felírható a megfelelő amplitúdója a forgó vektorok:

- gyorsulás amplitúdó; - amplitúdója a sebesség; - amplitúdója az elmozdulás; - az amplitúdó a hajtóerő. és

erő amplitúdója vektor megtalálható a jogállamiság vektor továbbá:

.

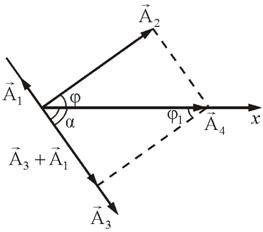
Ábra. 3.2 azt mutatja, hogy. Találunk A amplitúdó:

.

Így mind.

Állandó F0. β m, és az amplitúdó függ csak az arány a körfrekvencia ω a hajtóereje, és szabad, csillapítatlan rezgések ω0 rendszer.

A kezdeti szakaszban a kényszerrezgés megtalálható az expressziós

Ábra. 3.3 azt mutatja, hogy az erő, megelőzve a offset szögben, ami által meghatározott kifejezés

.

1) (a frekvencia a hajtóerő nulla), akkor

- statikus amplitúdó (rezgések nem fordul elő).

2) (nincs csillapítás). A növekvő ω (de) amplitúdó növekszik, és meredeken nő (). Ezt a jelenséget nevezzük rezonancia. A további növekvő ω () amplitúdó ismét csökken (ábra. 3.4).

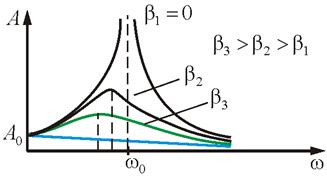
3) Az amplitúdó lesz maximális a minimális értékét a nevező. Ahhoz, hogy megtalálja az inflexiós pontot, hogy az első származékot ω radicand (3.3.7), és állítsa nullára:

4ω ≠ 0, és ezért a kifejezés zárójelben egyenlő nullával: