Hogyan lehet megtalálni az oldalán egy egyenlő szárú háromszög, ha adott a bázis

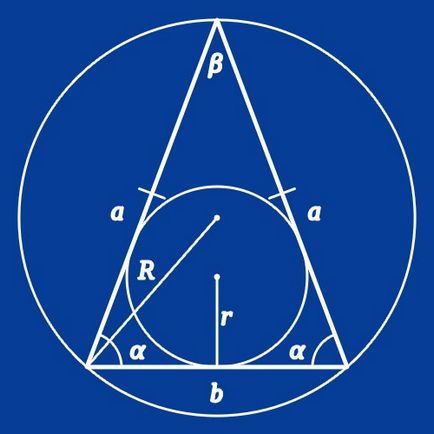
Jelöljük meg a oldalai és szögei egy egyenlő szárú háromszög. Hagyja a bázis b, oldalsó egy, a szögek az oldalsó szél és a bázis α, a bezárt szög bázis β, a h magasság.

Keresse az oldalsó a Pitagorasz-tétel, amely megállapítja, hogy a tér a átfogó egy derékszögű háromszög egyenlő az négyzetének összege a lábak - c ^ 2 = a ^ 2 + b ^ 2. Ha amellett, hogy a bázis egy egyenlő szárú háromszög ismert magassága, akkor ez egy egyenlő szárú háromszög tulajdonságokkal való medián és osztja a geometriai forma két egyenlő derékszögű háromszögek.

Helyettesítsük az egyenletben a kívánt értékeket. Tehát, ebben az esetben lenne: a ^ 2 = (b / 2) ^ 2 + H ^ 2. Megoldani az egyenletet: a = √ (b / 2) ^ 2 + H ^ 2. Más szóval, az oldalán a négyzetgyök kivonjuk az összeg fele a bázis, négyzetes, és a magasság, ami egyébként a téren.

Ha egy egyenlő szárú háromszög - téglalap alakú, sarkok annak bázis egyenlő 45 °. Számítsuk ki az oldalsó keresztül szinusz tétel: A / sin 45 ° = b / sin 90 °, ahol a B - a bázis, és - oldalsó, sin 90 ° egyenlő egységét. Az eredmény: a = b * sin 45 ° = b * √2 / 2. Azaz, az oldalsó oldalon a bázist megszorozza a négyzetgyök kettőnél osztva két.

A következő szinusztétel és abban az esetben, ha egy egyenlő szárú háromszög nem téglalap alakú. A bázis és a környező szöge α keresse az oldalsó. a = b * sinα / sinβ. A szög β kiszámított tulajdonságait háromszögek, amely megállapítja, hogy az összeg az összes háromszög szögei egyenlő 180 °: β = 180 ° - 2 * α.

Alkalmazzuk a koszinusz-tétel, amelyekkel összhangban oldalán a háromszög egyenlő a tér a négyzetösszeg a másik két fél mínusz kétszer a termék az adatok oldalán, szorozva a koszinusza a köztük lévő szög. Tekintettel a egyenlő szárú háromszög a fenti képlet a következő: a = b / 2cosα.

Ezen az ábrán, mint egy derékszögű háromszög róla, van egy egyértelmű képarány egymáshoz képest. Ismerve a ketten, akkor mindig talál egy harmadikat. Az, hogy ez hogyan lehet tenni, meg fogja tanulni az utasítás alatt kínálják.

Négyszögesítése mindkét lábát, majd add össze őket a2 + b2. Az eredmény a átfogója (bázis) szögletes c2. Ezután meg kell csak eltávolítani a gyökere az utolsó nap, és megállapította, az átfogó. Ez a módszer a legegyszerűbb és könnyen használható a gyakorlatban. Fontos a folyamat találni az oldalán a háromszög így - ne felejtsük el, hogy kibontsa a négyzetgyöke az előzetes eredmények, annak érdekében, hogy elkerüljék a leggyakoribb hibákat. A képlet származik a legismertebb a világon a Pitagorasz-tétel, amely minden forrás a következő: a2 + b2 = c2.

Osszuk az egyik lábát egy szinusz ellentétes vele szög sin α. Abban az esetben, ha egy ismert állapot oldala és a melléküregek, ebben a kiviteli alakban fogja találni a legtöbb elfogadható átfogója. A képlet ebben az esetben van egy nagyon egyszerű formában: c = a / sin α. Legyen óvatos, minden számítást.

Szorozzuk az oldalán egy két. Átfogója kiszámítani. Ez talán a legalapvetőbb módszert kell találni a megfelelő oldalára minket. De sajnos, ez a módszer csak egy esetben - ha van egy oldala átellenes fokos szögben intézkedés száma egyenlő a harminc. Ha bármely, akkor biztos lehet benne, hogy mindig lesz egy pontosan a fele az átfogója. Ennek megfelelően, akkor csak növelni kétszer, és a kész válasza.

Osszuk a befogó és a koszinusza a szög a vele szomszédos cos a. Ez a módszer csak abban az esetben, ha tudja, az egyik lábát, és a koszinusza a szög a szomszédos hozzá. Ez a módszer hasonlít a már bemutatott korábban, amely a használt lábban, de ahelyett, hogy a koszinusz - sine az ellenkező szögben. Csak itt a képlet ebben az esetben több egyéb módosított megjelenése: c = a / cos α. Ez minden.

Isosceles vagy egyenlő oldalú háromszög nevezzük, amelyben a hossza a két oldala azonos. Ha szükséges, kiszámításához a hossza az egyik oldalon ez a szám lehet használni a tudás értékeit szögek csúcsai kombinálva a hossza az egyik oldalon, vagy sugara a körülírt kör. Ezek a paraméterek Sokszög kapcsolódik tételei szinusz, koszinusz, és néhány más állandó arányban.

Kiszámításához az oldalsó hossza egyenlő szárú háromszög (b) az ismert hossza az alapja a körülmények (a), és az összeget a szomszédos szög (α) a koszinusz tétel. Ebből az következik, hogy meg kell osztani a hossza az ismert mellékhatások a kétszeres koszinusza a szög megadott feltételek: b = a / (2 * cos (α)).

Ugyanez elméletet alkalmazzák a fordított műveletet - számítási alap hossza (a) az ismert hosszúságú egy oldalsó (b) és a nagysága a szög (α) a két oldal között. Ebben az esetben, a tétel lehetővé teszi, hogy megkapjuk az egyenlőség, a jobb oldali része tartalmazza kétszer a termék hosszának az ismert mellékhatások a koszinusz a szög: a = 2 * b * cos (α).

Ha a oldalainak hossza eltérő (b) olyan körülmények között, kimutatták szögértéket közöttük (β), kiszámításához az alap hosszúsága (a) használja a szinusz tétel. Ebből a képletből következik, amely szerint kell kétszer oldalhosszúságú szorozva a szinusz fele ismert szög: a = 2 * b * sin (β / 2).

Sine tétel lehet használni a megállapítás a oldalhossza (b) egy egyenlő szárú háromszög, ha az ismert bázis hosszúságú (a) és a nagysága a szembenálló vele szöget (β). Ebben az esetben, megduplázódik a szinusz a fél szög formájában, és felosztják a kapott értéket a bázis hossza: b = a / (2 * sin (β / 2)).

Ha megközelítőleg egyenlő szárú háromszög alapja leírtak egy kört, amelynek a sugara (R) ismert, kiszámításához oldalainak hossza kell tudni a szög, az egyik csúcsot az ábra. Ha a feltételek információt tartalmaz az oldalai közötti szög (β), Számítsuk a bázis hosszúságú (a) munka sugara sokszög megduplázva az érték a szinusz a szög: a = 2 * R * sin (β). Ha egy adott értéke az a szög, a bázis (α), hogy megtalálják a hossza az oldalsó (b), egyszerűen cserélje a szög ebben a képletben: b = 2 * R * sin (α).