A megbízhatósági intervalluma az átlag (szórás ismert) MS Excel - kompatibilis a Microsoft
MS EXCEL össze egy konfidencia intervallum becslésére átlagértékeit az eloszlás esetében a ismert érték a diszperzió.
Cikk Statisztikák, mintavételi eloszlás és pontbecsléseket MS Excel definiálja a pontbecsléseit eloszlás paramétere (pont becslő). Azonban, mivel a véletlenszerű mintavételi pontot becslés nem esik egybe a értékelt paraméter és ésszerűbb, hogy jelezze a tartomány, amelyben a paraméter lehet ismeretlen a megfigyelt mintát x1. x2. xn. Ezért a cél a használata konfidenciaintervallumok lehet megszabadulni a bizonytalanság és lehetővé teszik a hasznos statisztikai következtetés.
Megjegyzés. Process adatokat összesíti mintában. ami egy valószínűségi nyilatkozatot a teljes lakosság számára. Statisztikai hívott végberendezés (statisztikai következtetés).
TIP. A konstrukció a megbízhatósági intervallum, tudnunk kell, hogy a következő fogalmakat:
Sajnos, az intervallumot, amelyben az ismeretlen paraméter lehet egybeesik a lehető legnagyobb variációs tartomány ezt a paramétert, mivel a megfelelő kiválasztása. ezért az értékelést paramétert. Akkor elő nem nulla valószínűséggel. Ezért találni határokat kell korlátozni változások az ismeretlen paraméter egy előre meghatározott valószínűségi előre.
Definíció: konfidencia intervallum az úgynevezett intervallum valószínűségi változó változás kotoryys adott valószínűségi, fedezi a valódi értéke a becsült eloszlás paramétere.
Ezt nevezik a valószínűsége, hogy egy adott megbízhatósági szinten (vagy bizalom valószínűség).
Rendszerint a bizalom szintje értékének 90%; 95%; 99%, legalább 99,9%, stb Például urovendoveriya 95% azt jelenti, hogy egy olyan esemény, amelynek valószínűsége 1-0,95 = 5%, a kutató úgy véli, hogy nem valószínű, vagy lehetetlen.
Megjegyzés: Annak a valószínűsége, ez az esemény az úgynevezett kiegészítő szignifikanciaszint vagy hiba az első ilyen. A részleteket lásd. Cikk szignifikancia szint és a megbízhatóság MS Excel.
Természetesen a választás a bizalmi szint attól függ a feladathoz. Így a fokú a bizalom és kíséretének a megbízhatóság a repülőgépek, persze, kell, hogy legyen nagyobb, mint a foka vevő bizalom a megbízhatóság az elektromos izzó.
Nyilatkozat a problémát
Tegyük fel, hogy egy populáció, amelynek normális eloszlás származó mintanagyság n. Feltételezzük, hogy a szórás ennek eloszlása ismert. Szükséges alapján ez a minta megbecsülni az ismeretlen középérték az eloszlás (μ, elvárás), és elkészítjük a megfelelő dvuhstoronniydoveritelny intervallumban.
pontbecslésével
Mint tudjuk, a központi határeloszlás tétel. statisztika
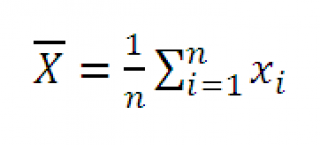
Megjegyzés: Mi a teendő, ha azt szeretnénk, hogy építsenek egy bizonytalansági intervallum forgalmazása esetén, amely nem yavlyaetsyanormalnym? Ebben az esetben jön, hogy segítsen a központi határeloszlás tétel. amely megállapítja, hogy egy elegendően nagy mintanagyság n eloszlásából nem yavlyayuschemsyanormalnym. szelektív eloszlása a statisztika HSR fog körülbelül megfelel a normál eloszláshoz paraméterekkel N (μ; σ 2 / n).
Tehát pont otsenkasrednegoznacheniya elosztó van - ez az átlagos minta értékét. azaz XCP. Most a megbízhatósági intervallum.
Építőipari megbízhatósági intervallum
Általában tudjuk, hogy a forgalmazás és paramétereit, ki tudjuk számítani a valószínűsége, hogy egy valószínűségi változó lesz az értéke a megadott intervallum minket. Most nem az ellenkezőjét: megtaláljuk a tartomány, amelybe egy véletlen változó fog esni egy adott valószínűség. Például, a tulajdonságait a normál eloszlás ismert, hogy egy 95% -os valószínűséggel, egy véletlenszerű változó elosztott normálisan. tartományba esik körülbelül +/- 2 szórásának átlaga (lásd. cikk a normális eloszlás). Ez az intervallum, szolgál majd, mint prototípust a megbízhatósági intervallum.
Most fogjuk megérteni, ha tudjuk, hogy a forgalmazás, kiszámítja ezt az intervallumot? A kérdés megválaszolásához meg kell adnia a eloszlás alakja és annak paramétereit.
elosztási forma tudjuk - ez a normális eloszlás (ne feledjük, hogy beszélünk szelektív raspredeleniistatistikiHsr).
μ paraméter ismeretlen (csak fel kell becsülni a megbízhatósági intervallum), de a pontszám XCP számított egy minta alapján, hogy lehet használni.
A második paraméter - a standard eltérést a mintavételi srednegobudem feltételezhető ismert. ez egyenlő a vizeletmintákban a ö / √n.
mert nem tudjuk, hogy μ, akkor épít egy sor +/- 2 szórás az átlagtól nem. Ismeretes az a HSR értékelést. Ie megbízhatósági intervallum számítás nem feltételezzük, hogy a HSR közé esik +/- 2 szórások μ egy 95% -os valószínűséggel, és azt feltételezzük, hogy az intervallum +/- 2 szórás a HSR egy 95% -os valószínűséggel fedezi μ - jelenti az általános a népesség, amelyből a mintát vették. Ez a két állítás ekvivalens, de a második utasítás lehetővé teszi számunkra, hogy építeni megbízhatósági intervallumok.
Ezen túlmenően, adjon meg egy értéket: a véletlen változó elosztott rendesen. 95% -os valószínűséggel az intervallumon belül 1960 +/- standard eltérésekkel, ahelyett +/- 2 szórás. Ez lehet kiszámítani a következő képlet segítségével NORM.ST.OBR = ((1 + 0,95) / 2). cm. Példa Fájl lapot intervallum.
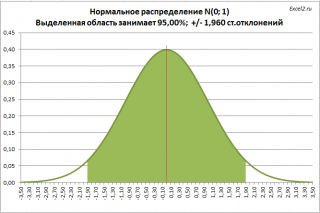
Most már tudjuk megfogalmazni egy valószínűségi nyilatkozat szolgál majd minket megalakult a megbízhatósági intervallum:
„Az a lehetőség, hogy a lakosság átlag a minta átlaga belül 1.960” a minta átlag szórása”. egyenlő 95%. "
A valószínűségi érték, mondta jóváhagyása, a név egy különleges bizalmi szintet, amely társítva van a szignifikancia szint α (alfa) az egyszerű kifejezést bizalom szintje 1 = -α. Ebben az esetben a szignifikancia szintet α = 1-0,95 = 0,05.
Most ennek alapján a valószínűségi kijelentések írja a kifejezést a számítás a megbízhatósági intervallum:
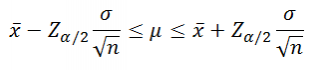
Megjegyzés. Felső α / 2 kvantilise meghatározza a szélessége a megbízhatósági intervallum standard otkloneniyahvyborochnogo közegben. A felső α / 2-kvantilstandartnogonormalnogo eloszlás mindig nagyobb, mint 0, ami nagyon kényelmes.
Ebben az esetben, α = 0,05, a felső α / 2--fraktil 1,960. Más szignifikancia szintek α (10%, 1%) magasabb, α / 2 kvantilZα / 2 számítható a következő képlet segítségével NORM.ST.OBR = (1-α / 2), vagy ha a konfidenciaszint ismert. NORM.ST.OBR = ((1 + ur.doveriya) / 2).
Általában az építőiparban konfidenciaintervallumai a becslések átlaga csak a felső α / 2-kvantilis és ne használja az alsó α / 2 quantile. Ez azért lehetséges, mert standartnoenormalnoe eloszlása szimmetrikus az X-tengely (a sűrűség eloszlása szimmetrikus az átlagos, azaz 0). Ezért nincs szükség a kiszámításához az alsó α / 2-kvantilis (úgynevezett egyszerűen a / 2 kvantilis), mint ez egyenlő a felső α / 2-kvantilis egy mínusz jelet.
Emlékezzünk, hogy annak ellenére, hogy az alak a eloszlása X megfelelő véletlen értéket HSR van allokálva priblizitelnonormalno N (μ; σ 2 / n) (lásd a cikk a CLT.). Ezért általában a fenti kifejezés a megbízhatósági intervallum csak közelítés. Ha az x értéke egy normális eloszlás N (μ; σ 2 / n), akkor a kifejezés a konfidenciaintervallum pontos.
Kiszámítása a megbízhatósági intervallum MS Excel
Mi a probléma megoldására.
elektronikus alkatrész válaszidő, hogy a bemeneti jel egy fontos jellemzője az eszköz. A mérnök akar építeni egy megbízhatósági intervallum átlagos válaszidő 95% -os megbízhatósági szinten. mérnök tudja, a korábbi tapasztalat, hogy a szórása a válaszidő 8 ms. Köztudott, hogy a válaszidő értékelésére mérnök készült 25 mérés középértéke 78 ms.
Határozat. A mérnök meg akarja ismerni a válaszidő az elektronikus készülék, de rájön, hogy a válaszidő nincs rögzítve, mint egy véletlen változó, amely saját forgalmazás. Tehát a legjobb, hogy lehet remény az, hogy meghatározza a paramétereket és az alakja ennek eloszlása.
Sajnos a feltétele a feladat válaszidő eloszlása formában nem tudjuk (nem kell, hogy normális). Másodlagos, azaz elvárás. Ez az eloszlás is ismert. Úgy ismert, csak annak szórása σ = 8. Ezért, bár nem tudjuk kiszámítani a valószínűség és a bizalom intervallumban.
Azonban annak ellenére, hogy nem tudjuk, vremeniotdelnogo válasz forgalmazás. Tudjuk, hogy megfelelően a CLT. raspredeleniesrednego szelektív válaszidő közelítőleg normális (feltételezzük, hogy a PTC feltételek teljesülnek, mivel a minta mérete elég nagy (n = 25)).
Továbbá, az átlagos ezen eloszlás egy átlagos értéke az elosztó egység választ, azaz μ. A standard deviáció ezen eloszlás (σ / √n) lehet kiszámítani a következő képlettel = 8 / SQRT (25).
Az is ismert, hogy egy mérnök pontbecslése paraméter μ egyenlő 78 msec (HSR) kapunk. Ezért most már számítani a valószínűsége, mert tudjuk, hogy a eloszlás alakja (normál) és annak paraméterei (XCP és σ / √n).
A mérnök akarja tudni az elvárás μ eloszlása reakcióidőt. Mint már említettük, ez μ egyenlő a középértéke az eloszlás átlagos válaszidő. Ha használjuk a normális eloszlás N (HSR; σ / √n), majd a kívánt μ lesz a tartományban +/- 2 * σ / √n valószínűséggel körülbelül 95%.
A szignifikancia szint egyenlő 1-0,95 = 0,05.
Végül azt találtuk, hogy a bal és jobb határa a megbízhatósági intervallum.
Bal határ = 78 NORM.ST.OBR (1-0,05 / 2) * 8 / SQRT (25) = 74,864
Jobb határ = 78 + NORM.ST.OBR (1-0,05 / 2) * 8 / SQRT (25) = 81,136
Bal határ = NORM.OBR (0,05 / 2; 78; 8 / SQRT (25))
Jobb határ = NORM.OBR (1-0,05 / 2; 78; 8 / SQRT (25))
Válasz. konfidencia intervallum 95% -os megbízhatósági szint és σ = 8 ms 78 ms +/- 3136.
A példa fájl egy lapon alakú létrehozott Sigma ismert kiszámításának és építése dvuhstoronnegodoveritelnogo intervallum tetszőleges minták σ és adja meg a szignifikancia szintjét.
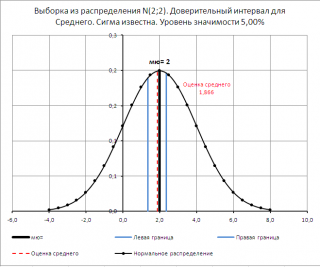
DOVERIT.NORM funkció ()
Ha a minta értékek közötti tartományban B20: B79. és a szint a szignifikancia egyenlő 0,05; képlet MS EXCEL:
= ÁTLAG (B20: B79) -DOVERIT.NORM (0,05; σ, COUNT (B20: B79))
vissza a bal széle a megbízhatósági intervallum.
Ez ugyanaz a határ lehet kiszámítani a következő képlet segítségével:
= ÁTLAG (B20: B79) -NORM.ST.OBR (1-0,05 / 2) * σ / SQRT (COUNT (B20: B79))